With H2O GPU Edition, H2O.ai seeks to build the fastest artificial intelligence (AI) platform on GPUs. While deep learning has recently taken advantage of the tremendous performance boost provided by GPUs, many machine learning algorithms can benefit from the efficient fine-grained parallelism and high throughput of GPUs. Importantly, GPUs allow one to complete training and inference much faster than possible on ordinary CPUs. In this blog post, we’re excited to share some of our recent developments implementing machine learning on GPUs.
Consider generalized linear models (GLMs), which are highly interpretable models compared to neural network models. As with all models, feature selection is important to control the variance. This is especially true for large number of features; [latex]p > N[/latex], where [latex]p[/latex] is the number of features and [latex]N[/latex] is the number of observations in a data set. The Lasso regularizes least squares with an [latex]\ell_1[/latex] penalty, simultanously providing shrinkage and feature selection. However, the Lasso suffers from a few limitations, including an upper bound on variable selection at [latex]N[/latex] and failure to do grouped feature selection. The elastic net regression overcomes these limitation by introducing an [latex]\ell_2[/latex] penality to the regularization [1]. The elastic net loss function is as follow:
![]()
, where [latex]\lambda[/latex] specifies the regularization strength and [latex]\alpha[/latex] controls the penalty distribution between [latex]\ell_1[/latex] and [latex]\ell_2[/latex].
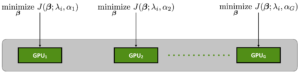
Multiple GPUs can be used to fit the full regularization path (i.e. [latex]\lambda[/latex] sweep) for multiple values of [latex]\alpha[/latex] or [latex]\lambda[/latex].

Below are the results of computing a grid of elastic net GLMs for eight equally spaced value of [latex]\alpha[/latex] between (and including) 0 (full [latex]\ell_2[/latex]) and 1 (full [latex]\ell_1[/latex]; Lasso) across the entire regularization path of 100 [latex]\lambda[/latex] with 5-fold cross validation. Effectively, about 4000 models are trained to predict income using the U.S. Census data set (10k features and 45k records).

Five scenarios are shown, including training with two Dual Intel Xeon E5-2630 v4 CPUs and various numbers of P100 GPUs using the NVIDIA DGX-1. The performance gain of GPU-acceleration is clear, showing greater than 35x speed up with eight P100 GPUs over the two Xeon CPUs.
Similarily, we can apply GPU acceleration to gradient boosting machines (GBM). Here, we utilize multiple GPUs to train separate binary classification GBM models with different depths (i.e. max_depth = [6,8,10,12]) and different observation sample rates (i.e. sample_rate = [0.7, 0.8, 0.9, 1]) using the Higgs dataset (29 features and 1M records). The GBM models were trained under the same computing scenarios as the GLM cases above. Again, we see substantial speed up of up to 16x when utilizing GPUs.

GPUs enable a quantum leap in machine learning, opening the possibilities to train more models, larger models, and more complex models — all in much shorter times. Iteration cycles can be shortened and delivery of AI within organizations can be scaled with multiple GPU boards with multiple nodes.
The Elastic Net GLM and GBM benchmarks shown above are straightforward implementations, showcasing the raw computational gains of GPU. On top of this, mathematical optimizations in the algorithms could result in even more speed-up. Indeed, the H2O CPU-based GLM is sparse-aware when processing the data and our newly-developed H2O CPU-based GLM implements mathematical optimizations, which lead it to outperform a naive implementation by a factor of 10 — 320s for H2O CPU GLM versus 3570s for naive CPU GLM. The figure below illustrates the H2O CPU GLM and H2O GPU GLM against other framework implementations (tensorflow uses stochastic gradient descent and warmstart, while H2O CPU version and Scikit Learn use a coordinate descent algorithm, while H2O GPU GLM uses a direct matrix method that is optimal for dense matrices — we welcome improvements to these other frameworks, see http://github.com/h2oai/perf/ ).

H2O GPU edition captures the benefits from both GPU acceleration and H2O’s implementation of mathematical optimizations taking the performance of AI to a level unparalleled in the space. Our focus on speed, accuracy and interpretability has produced tremendously positive results. Benchmarks presented in this article are proofs of such, and we will have more benchmark results to present in the near future. For more information about H2O GPU edition, please visit www.h2o.ai/gpu.
[1] H. Zou and T. Hastie. “Regularization and variable selection via the elastic net” https://web.stanford.edu/~hastie/Papers/B67.2%20(2005)%20301-320%20Zou%20&%20Hastie.pdf